Geometry Problem 1371: Equilic Quadrilateral, 120 Degrees, Congruence, Midpoint, Diagonal, Equilateral Triangle, Parallel, Collinearity

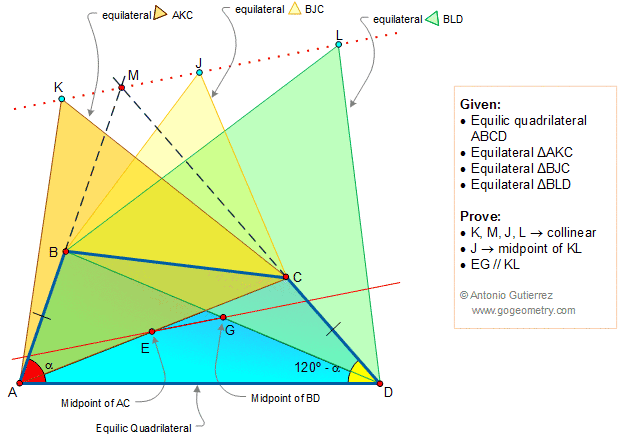
In the figure below ABCD is an equilic quadrilateral. If AB meet DC in M, equilateral triangles AKC, BJC and BLD are drawn away from AD, and E and G are the midpoint of the diagonals AC and BD, prove that K, M, J and L are collinear, J is the midpoint of KL and EG and KL are parallel lines.

Geometry Problem 1371 Equilic quadrilateral