
|
|

HTML5 Animation for iPad and Nexus: Nine-Point Center, Nine-Point Circle, Euler Line, Step by Step Interactive Illustration. Orthocenter, Circumcenter, Centroid, Midpoint.
Triangle centers,
Nine-Point Circle, Euler Line,
Altitudes, Midpoints.
Orthocenter, Circumcenter,
Centroid and more, brought to life
With HTML5 for all.
Click the Next button below to start the illustration.
|
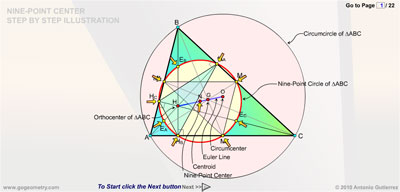
The Nine-point center is the center of
the nine-point circle. The Nine-Point Circle of triangle ABC
with orthocenter H is the circle that passes through the
feet of the altitudes HA, HB and HC to the three sides, the
midpoints MA, MB and MC of those sides, and the Euler Points
EA, EB and EC, which are the midpoints of the segments AH, BH, and CH,
respectively. Euler line is the line passing through the
orthocenter H, the nine-point center N, the
centroid G, and the
circumcenter O of any triangle ABC. Click the Next button
above to start the step-by-step illustration.
-
The nine-point center N
is the midpoint of the line HO.
-
The distance from the
orthocenter H to the centroid G is twice the
distance from the circumcenter O to the centroid
G.
-
The nine-point center N
is the circumcenter of the medial triangle MAMBMC.
-
The nine-point center N
is the circumcenter of the orthic triangle HAHBHC.
The nine-point circle is also known as
Euler's circle and Feuerbach's circle.
Leonhard Euler showed in 1765 that the
nine-point circle bisects any line from the orthocenter to a
point on the circumcircle. In 1822
Karl Feuerbach discovered
that any triangle's nine-point circle is externally tangent to
that triangle's three
excircles and internally tangent to its
incircle.
See also:
Nine-Point Circle, Euler Line in Instagram.
|
|
|
|
|
 |