|
Leonhard Euler
(Swiss mathematician and physicist, 1707-1783) and his beautiful and
extraordinary formula that links the 5 fundamental constants in
Mathematics, namely, e, the base of the natural logarithms, i,
the square root of -1, Pi, the ratio of the circumference of a
circle to its diameter, 1 and 0, together!
Euler's Equation or Identity
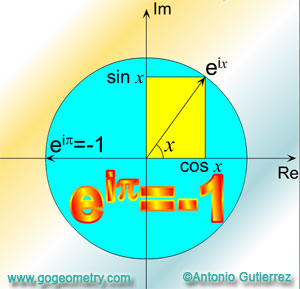
Euler's formula
is a mathematical formula in complex analysis that
shows a deep relationship between the trigonometric
functions and the complex exponential function.
Euler's formula states that, for any real number x:
(1)
\(e^{ix}=\cos x+i\cdot \sin x\) (Euler's formula)
where:
Euler's equation or
identity is a special case of the Euler'
formula, where:
(2)
\(x=\pi \)
By substitution in (1):
(3)
\(e^{i\pi }=\cos \pi +i\cdot \sin \pi \)
(4)
\(e^{i\pi }=-1+0 \)
(5) Therefore:
\(e^{i\pi }=-1 \) (Euler's Equation or Identity)

Benjamin Peirce
(1809-1880, American mathematician, professor at Harvard) gave a
lecture proving "Euler's equation", and concluded:
"Gentlemen, that is
surely true,
it is absolutely
paradoxical;
we cannot understand
it,
and we don't know
what it means.
But we have proved
it,
and therefore we
know it must be the truth."
Reference: The
Changing Shape of Geometry. Celebrating a Century of Geometry
and Geometry Teaching. Edited on behalf of The Mathematical
Association UK by Chris Pritchard. Cambridge University Press,
(Cambridge 2003).
|