|
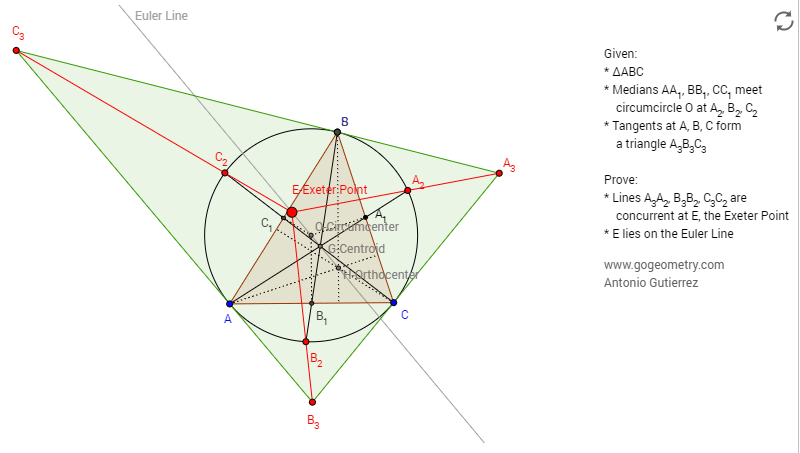
Given a triangle ABC (see the dynamic figure
below), Medians AA1, BB1, and CC1, meet the circumcircle O at A2, B2, and C2, respectively. Tangents at A, B, and C form a triangle A3B3C3. Prove that (1) Lines A3A2, B3B2, and C3C2
are concurrent at a point E, called the Exeter point.
(2) E lies on the Euler line.
See
also:
Exeter Point Puzzle.
Reference
Kimberling, Clark. "Encyclopedia
of Triangle Centers: X(22)"
Dynamic Geometry Environment (DGE) or Interactive Geometry Software
(IGS) of the Exeter Point
The interactive demonstration above was created with GeoGebra.
To stop/play the animation: tap the icon in the
lower left corner.
To reset the interactive figure to its initial state: tap the icon in the
upper right corner.
To manipulate the interactive figure: tap and drag points or lines.
GeoGebra
GeoGebra is free
and multi-platform dynamic mathematics software for all levels of
education that joins geometry, algebra, tables, graphing, statistics and
calculus application, intended for teachers and students.
Static Diagram of Exeter Point
|