Unraveling the Incircle Mystery: A Tangent-Midpoint Connection in Triangle Geometry
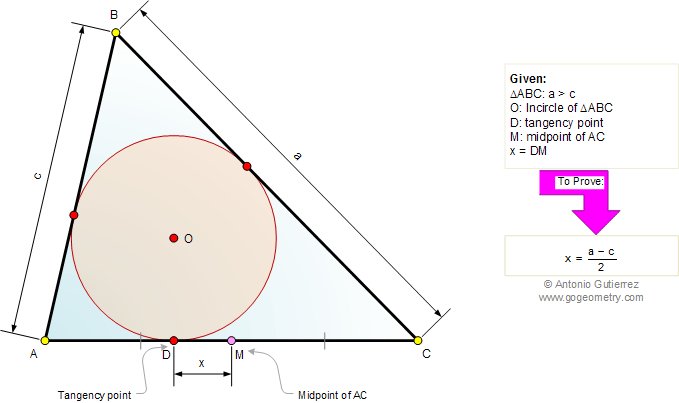
Embark on a journey through the elegance of geometry with this captivating challenge. In triangle ABC, where the length of side BC exceeds that of side AB, the incircle meets side AC at point D. Your task is to prove that the distance from D to the midpoint M of AC is exactly half the difference between the lengths of BC and AB.
This problem invites you to explore the harmonious interplay between the incircle, midpoints, and the sides of a triangle.
It tests your understanding of key geometric principles and hones your logical reasoning, making it a perfect mental exercise for students and enthusiasts alike.
Dive into the proof and discover the hidden balance within triangle ABC.
Are you ready to master the incircle mystery and unlock its elegant solution?
Problem Statement
In triangle ABC, the incircle
touches AC at D. Prove that the distance between D and the
midpoint M of AC is half the difference between BC and AB
|