|
The figure shows a cyclic quadrilateral ABCD
with circumcenter O.
Diagonals AC and BD meet at M. If E, F, G, and H are the circumcenters of
triangles AMB, BMC, CMD, and AMD, respectively, prove that lines EG, FH,
and MO are concurrent at the same point P.
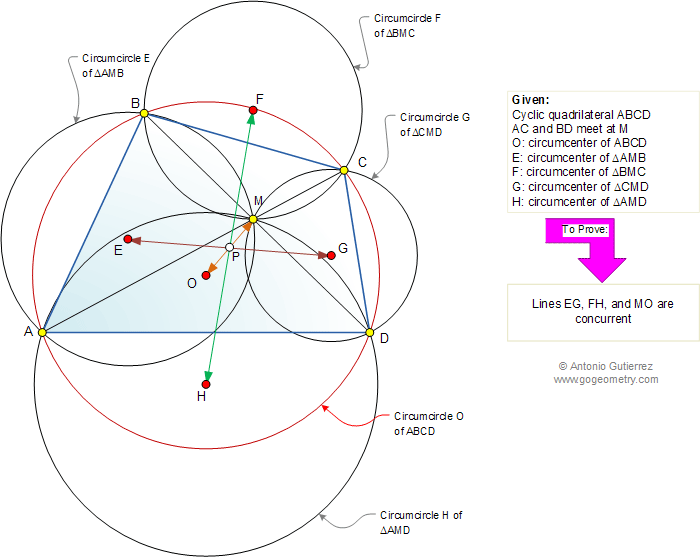
|