Math: Geometry Problems 577. Activate Flash plug-in or JavaScript and reload to view
the Math Geometry Proposed Problems, online geometry classes, Geometry help,
College, Online Learning. Site created and maintained by Antonio
Gutierrez.
Problem 577: Isosceles triangle, Midpoint, Perpendicular, Concyclic
points, Circle.
Level: Math Education, High School, SAT Prep, College
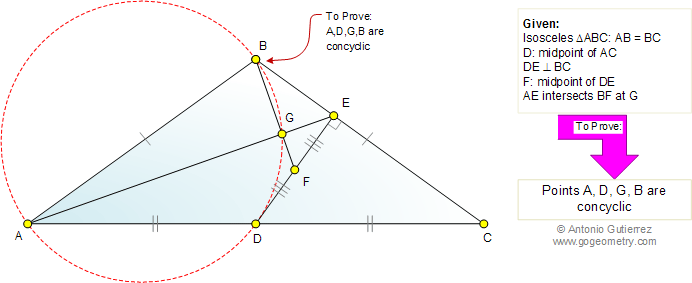
The figure shows an isosceles triangle ABC
(AB = BC). D is the midpoint of AC and DE is perpendicular to BC. F is
the midpoint of DE and AE intersects BF at G. Prove that the points A, D,
G, and B are concyclic (lie on a same circle).
