Geometry Problem 371: Unleashing the Power of Proof - Conquer the Square, Inscribed Circle, Triangle, and Area with Confidence!

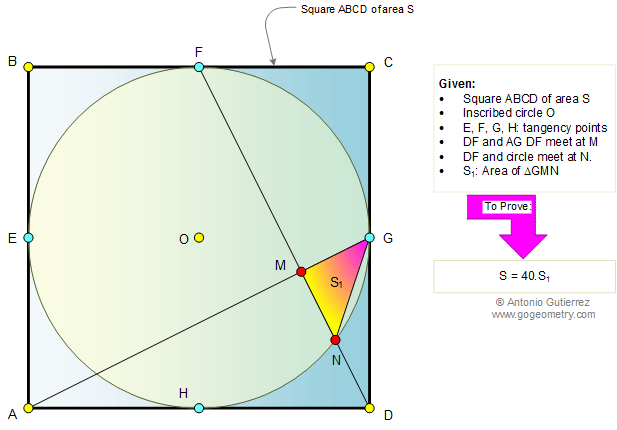
In the given figure, a circle O is inscribed in a square ABCD of area S. The tangency points of the circle with the sides of the square are labeled E, F, G, and H. Point M is the intersection of lines DF and AG, and point N is the intersection of line DF and circle O. Let S₁ denote the area of triangle GMN. Prove that S equals 40 times S₁.

Square holds circle tight,
Triangle forms at their meet.
Area, what's the plight?

See also:
Typography of problem 371.