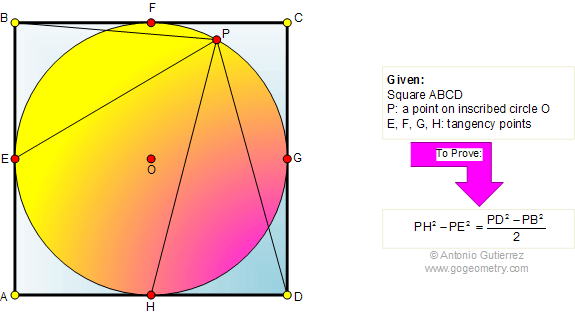
The figure shows a square ABCD with P
on the inscribed circle O. If E, F, G, and H are the tangency
points, prove that
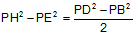 .
.
Thematic Poem:
Unraveling the Mystery: The Relationship Between Points on an Inscribed Circle and Tangency Points in a Square
Amidst the squares and angles of our
minds,
Lies a mystery waiting to be found,
A hidden path
that none yet unwinds,
A puzzle yet to be unbound.
Discovering the relationship between,
Distances of a point on
circle's arc,
To tangency points and vertices seen,
A
revelation, a brand-new spark.
The inscribed circle, a
central guide,
With its point in question, a starting place,
We take a journey with eyes open wide,
And unravel a puzzle
with skill and grace.
With each step forward, we find a
clue,
And piece by piece, the picture emerges clear,
A new
perspective that once was askew,
Now seen with clarity,
without a single tear.
The distance to vertices, the
tangency points,
All speak to us in silent code,
A
language that our heart anoints,
As we walk the path, on this
quest we strode.
The thrill of discovery, a journey
worthwhile,
A quest that feeds the mind and soul,
The
beauty of numbers, an endless pile,
As we uncover mysteries,
a story untold.
In this journey, we find a new friend,
A geometry that speaks to us in rhyme,
A love for numbers,
that never ends,
And a journey that transcends time.

