|
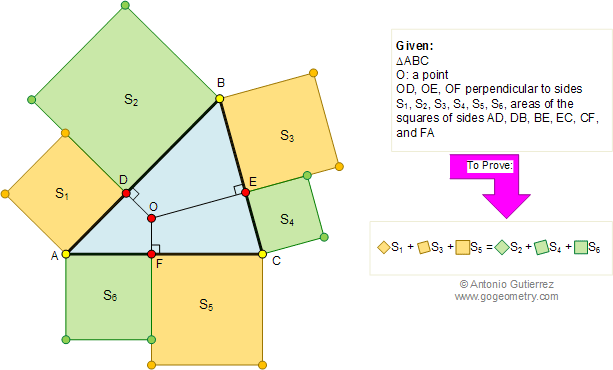
Problem 273: Triangle, Perpendiculars, Area of Squares
In the figure below, from a point O inside or outside of a triangle ABC, perpendiculars are drawn to the sides meeting AB, BC, and AC , at points D, E, and F, respectively. If S1, S2, S3, S4, S5, and S6 are the areas of the squares of sides AD, DB, BE, EC, CF, and FA, respectively, prove that S1 +S3 + S5 = S2 + S4 + S6.
|
Recent Additions
|