|
Geometry
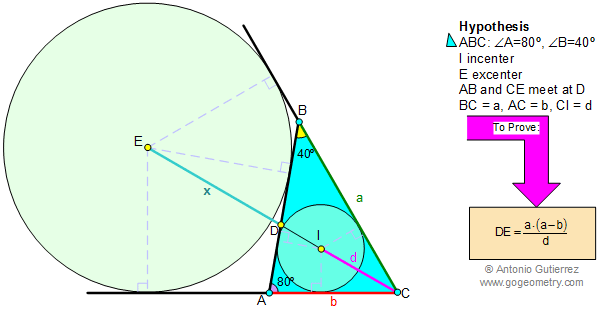
Help: Proposed Problem 40. Level: High School, SAT
Prep, College |
|
|
|
SUGGESTIONS for
Problem 40
|
|
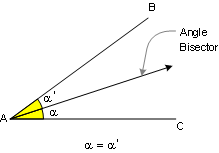
DEFINITION 1. Angle is the figure formed by two
rays with a common end point.
Congruent angles are angles
that have the exact same measure (the same number of degrees).
Angle Bisector is a ray that
divides the angle into two congruent adjacent angles.
|
|
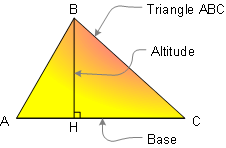
DEFINITION 2. Triangle is a three side polygon.
Polygon is a closed plane figure with
n
sides. Altitude is the perpendicular line segment from
one vertex to the line that contains the opposite side.
|
|
PROPOSITION 1. The sum of the measures of the three
angles of a triangle is 180.
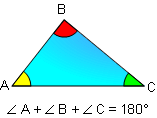
|
|
PROPOSITION 2. The measure of an exterior angle of a
triangle equals the sum of the measures of the two
non-adjacent interior angles.
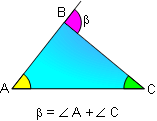
|
|
PROPOSITION 3. The sum of the measures of the acute
angles of a right triangle is 90 (complementary).
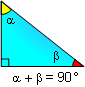
|
|
PROPOSITION 4. Triangle Congruence A.S.A. If two
angles and the included side of one triangle are congruent to
the corresponding parts of another, then the triangles are
congruent.
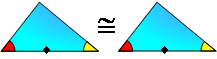
|
|
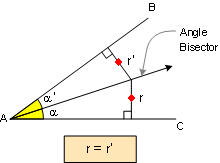
PROPOSITION 5. Any point on the bisector of
an angle is equidistant from the sides of the angle. Also
converse
 |
|
PROPOSITION 6. Triangle Congruence S.A.S. If
two sides and the included angle of one triangle are
congruent to the corresponding parts of another, then the
triangles are congruent.
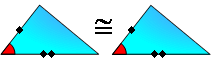
|
|
PROPOSITION 7. Isosceles triangle: If two sides of
a triangle are congruent, the angles opposite these sides are
congruent. Also converse.

|
|
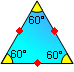
PROPOSITION 8. An equilateral triangle is equiangular: 60-60-60. Also converse.
|
|
DEFINITION 3. Circle is the set of all points in a
plane that are at the same distance from a fixed point
called the center.
Tangent of a circle is a
line that touches the circle at one and only one point no
matter how far produced.
PROPOSITION 9. If a line is
tangent to a circle, it is perpendicular to a radius at the
point of tangency.
 |
|
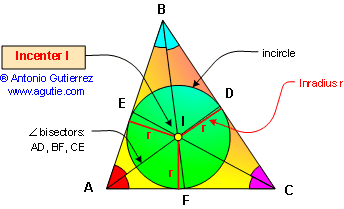
PROPOSITION 10. The bisectors
AD, BF and CE of the angles of a triangle ABC meet in a
point I, which is equidistant from the sides of the
triangle.
The incircle is the inscribed
circle of a triangle. The center of the incircle is called
the incenter, and the radius of the circle is called the
inradius.
|
|
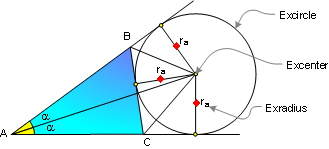
PROPOSITION 11. An excircle of the
triangle is a circle lying outside the triangle, tangent to
one of its sides and tangent to the extensions of the other
two.
The center of an excircle is the
intersection of the internal bisector of one angle and the
external bisectors of the other two.
The center of an excircle is called
the excenter, and the radius of the circle is called the
exradius.
|
|
PROPOSITION 12. A central angle is measured by its
intercepted arc.
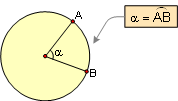
|
|
PROPOSITION 13. An inscribed angle is measured by
one-half its intercepted arc.
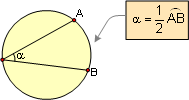
|
|
DEFINITION 4. A cyclic quadrilateral is a
quadrilateral whose vertices all lie on a single circle.
PROPOSITION 14.1
Opposite angles of a cyclic
(inscribed) quadrilateral are supplementary. Also converse.
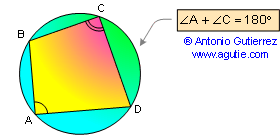
PROPOSITION 14.2 A quadrilateral is cyclic if one side subtends
congruent angles at the two opposite vertices. Also
converse.
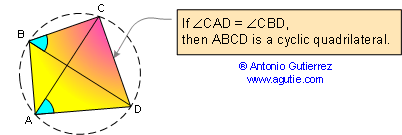
|
|
DEFINITION 5. Similar Triangles
are triangles whose corresponding angles are congruent and whose
corresponding sides are in proportion.

PROPOSITION 15. Triangle Similarity AA. If two
angles of one triangle are congruent to two angles of another
triangle, the two triangles are similar.
|