 |

|
|

Problema de Geometría 735 (ESL): Triangulo, Alturas, Órtico,
Perpendiculares, Semiperímetro, Ortocentro.
Nivel: Educación Secundaria, Pre-Universitaria, Bachillerato.
|
|
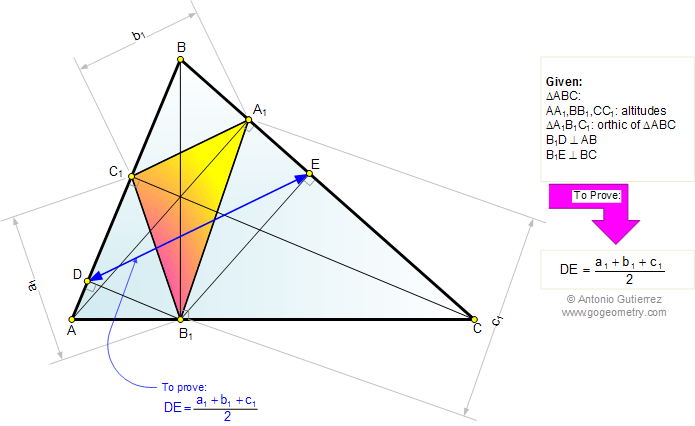
En la figura, ABC es un triangulo de alturas AA1, BB1
y CC1. Si B1D
es perpendicular a AB, y B1E es perpendicular a BC,
demostrar que DE es igual al semiperímetro del triangulo A1B1C1.
Nota: El triangulo A1B1C1 se llama
triangulo Órtico del triangulo ABC.
|
|
|
|
|
|
 |
 |