|
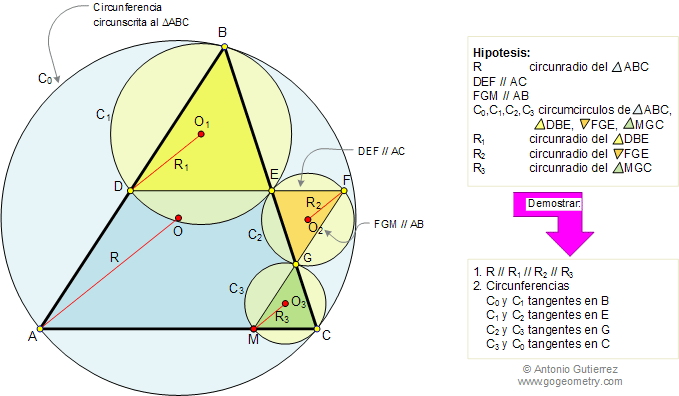
En el triangulo ABC (ver figura), las líneas FED y FGM son paralelas
a AC y AB, respectivamente. Si C0, C1, C2,
y C3, son las circunferencias circunscritas a los
triángulos ABC, DBE, FGE y MGC, respectivamente y R, R1,
R2,
y R3, son los circunradios que pasan por A, D, F y M,
respectivamente, demostrar que: (1) R, R1, R2,
y R3 son paralelos; (2) C0 y C1
son tangentes en B; C1 y C2 son tangentes
en E; C2 y C3 son tangentes en G; C3
y C0 son tangentes en C.
|