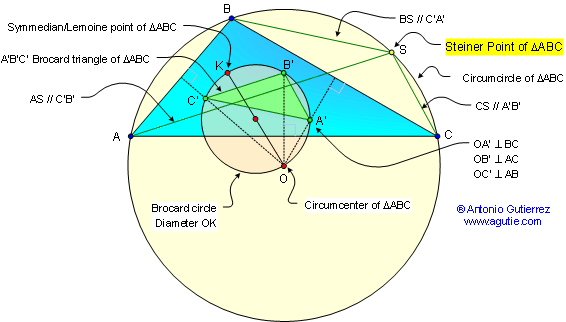
The Steiner point of a triangle ABC is constructed as follows: First, let O be the circumcenter and K the symmedian (or Lemoine) point of ABC. The circle having segment OK as diameter is the Brocard circle. The line through O perpendicular to line BC passes through the Brocard circle in another point, A'; similarly, obtain points B' and C'. The triangle A'B'C' is the  Brocard triangle. Now, construct the line through A parallel to line B'C', the line through B parallel to line C'A', and the line through C parallel to line A'B'. These three lines concur in the Steiner point, S. It lies on the circumcircle.
 

The point was studied by Jakob Steiner (1796-1863) Swiss mathematician.