Geometry Problem 1419: Triangle, Altitude, Circumcircle, Incenter, Inradius, Perpendicular, Angle Bisector, Midpoint
Proposition
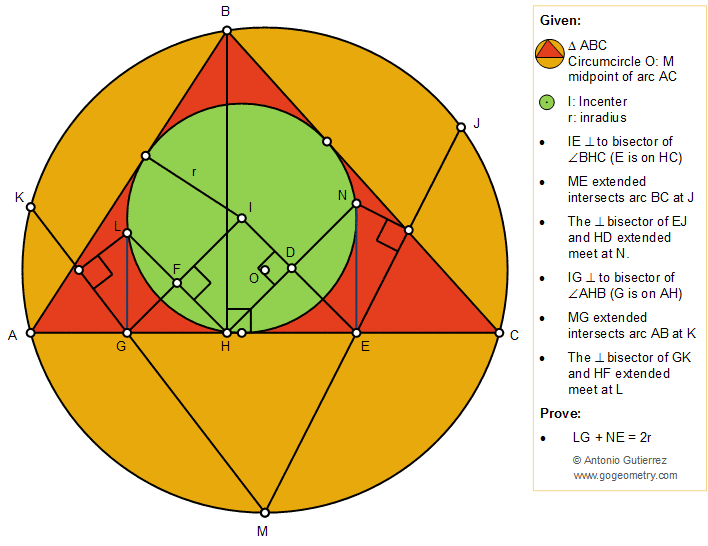
The figure below shows a triangle ABC
with the incenter I, inradius r, the altitude BH, the circumcircle O and
the midpoint M of arc
AC. A line segment through I and perpendicular to the bisector of the
angle BHC at D intersects HC at E. ME extended intersects arc BC
at J. HD extended and the perpendicular bisector of EJ meet at N. A line
segment through I and perpendicular to the bisector of the angle AHB at F intersects
AH at G. MG extended intersects arc AC
at K. HF extended and the perpendicular bisector of GK meet at L. Prove that
LG + NE = 2r.
Geometric Art of Problem 1419: Sketching, Typography, iPad Apps

See also: Typography and poster of problem 1408.