|
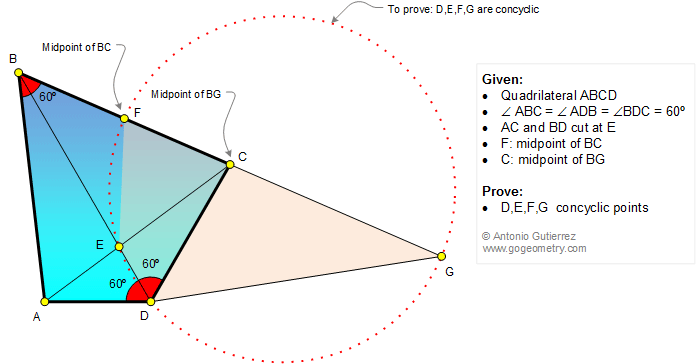
In a quadrilateral ABCD, angle ABC = angle ADB = angle BDC = 60 degrees.
The diagonals cut at E. The midpoint of BC is F and BC is extended to G such that C is the midpoint of BG
. Prove that D,E,F,G are concyclic points.
This entry contributed by Sumith Peiris, Moratuwa, Sri Lanka.
|

