 |

|
Geometry Problem 1168: Construction
of the Inscribed Circle of the Arbelos,
Semicircles, Diameter, Circle,
Triangle, Circumcircle, Tangent. Level: High School, College, Math Education,
Tutoring
< PREVIOUS PROBLEM |
NEXT PROBLEM >
|
|
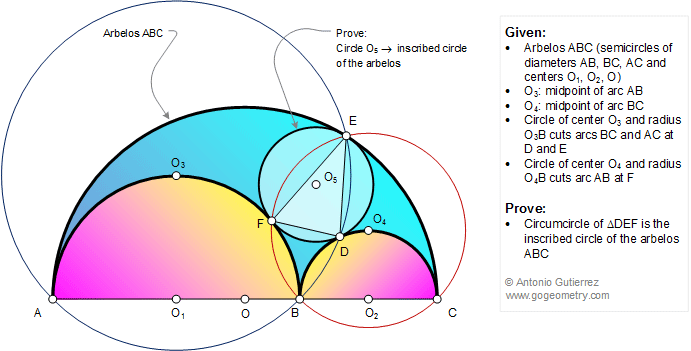
The figure shows an arbelos ABC (AB, BC, and AC are semicircles
of centers O1, O2, and O). O3
and O4 are the midpoints of arcs AB and BC,
respectively. Circle of center O3 and radius O3B cuts arcs BC
and AC at D and E, respectively. Circle of center O4
and radius O4B cuts arc AB at F. Prove that the
circumcircle of triangle DEF is the inscribed circle of the
arbelos ABC.. See also:
Isolines Artwork Problem
1168.
|
|
|
|
|
|
 |
 |