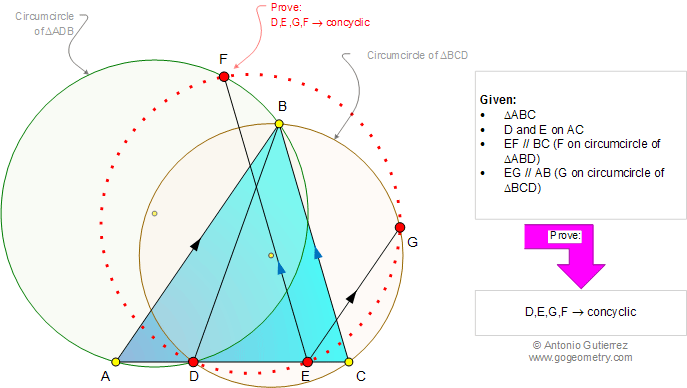
Math: Geometry Problem 1002: Triangle, Circle, Circumcircle, Cevian, Parallel Lines, Cyclic Quadrilateral, Concyclic Points. Level: School, College.

The figure below shows a triangle ABC with D and E on AC. EF is parallel to BC (F on circumcircle of triangle ABD) and EG is parallel to AB (G on circumcircle of triangle BCD). Prove that points D, E, G, and F are concyclic.