|
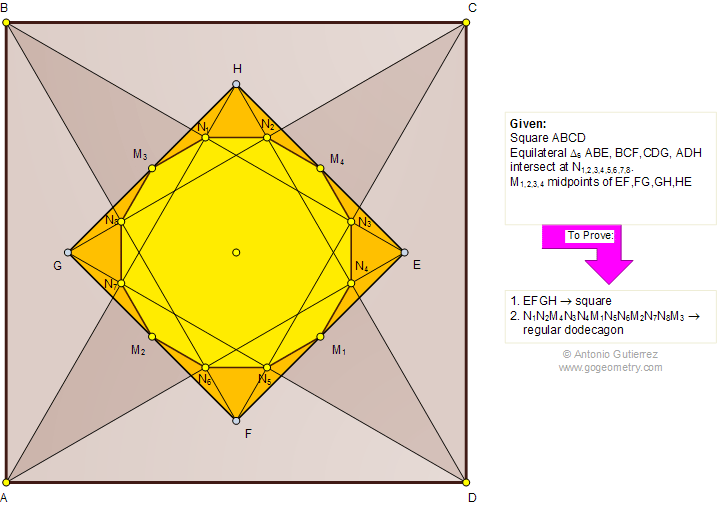
In the diagram below, ABCD is a square with the equilateral triangles ABE, BCF, CDG, and ADH. Prove that (1) EFGH is a square; (2) The 8 intersections (N1,2..8) of the equilateral triangles and the midpoints (M1,2,3,4) of
the sides of EFGH form a regular dodecagon.
See also:
Problem 1358: Square, Regular Dodecagon
Problem 1357: Regular Dodecagon, Concurrency, Collinearity
Problem 1323: Square, Regular Dodecagon
|