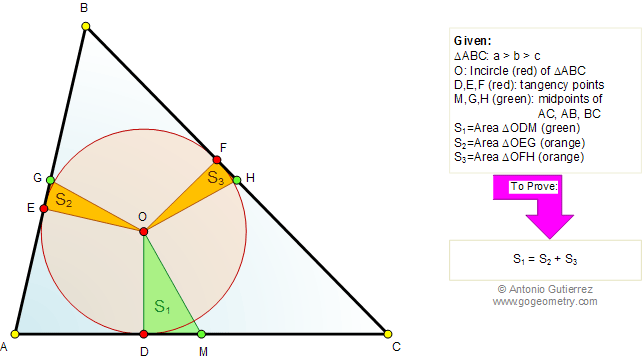
|
The figure shows a triangle ABC (BC > AC >
AB). The incircle O is tangent to AC, AB, and BC at D, E, and F,
respectively. If M, G, and H are the midpoints of AC, AB, and BC,
respectively, prove that the area of triangle ODM is equal to the sum of
areas of triangles OEG and OFH.
|