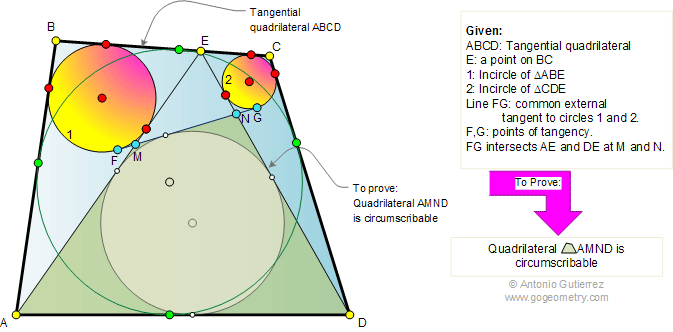
 |
|
Problem 352. Tangential quadrilateral, Incircles, Common tangent,
Circumscribable or Tangential quadrilateral.
The figure shows a tangential
quadrilateral ABCD with a point E on side BC. Circles 1 and 2
are the incircles of triangles ABE and CDE, respectively. FG is
the common tangent to circles 1 and 2. FG intersects to AE and
DE at M and N, respectively. Prove that the quadrilateral AMND
is circumscribable or tangential (sides all lie tangent to a
single circle inscribed within the quadrilateral).
Geometry problem solving
Geometry problem solving is one of the most challenging skills for students to learn. When a problem requires auxiliary construction, the difficulty of the problem increases drastically, perhaps because deciding which construction to make is an ill-structured problem. By “construction,” we mean adding geometric figures (points, lines, planes) to a problem figure that wasn’t mentioned as "given."
|
Recent Additions
|
