 |
|
|
Problem 350. Triangle, Cevian, Incircles, Tangents, Tangency Points,
Angles.
Level: High School, College, SAT Prep.
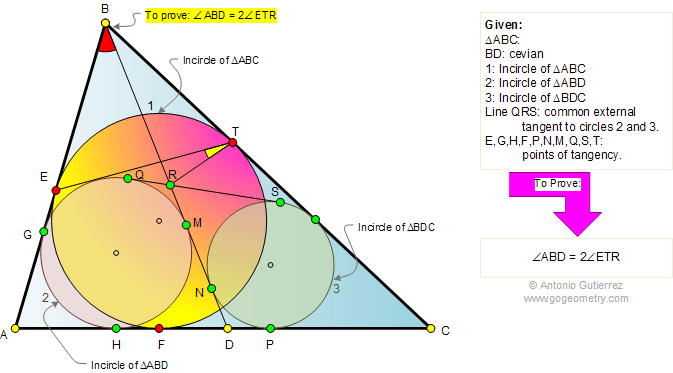
The figure shows a triangle ABC
with point D on side AC. Circles 1, 2, and 3 are the incircles
of triangles ABC, ABD, and BDC, respectively. QS is the common
tangent to circles 2 and 3. QS intersects to cevian BD at R. If
E,G,H,F,P,N,M,Q,S, and T are points of tangency, prove that the
angle ABD is double the angle ETR.
Geometry problem solving
Geometry problem solving is one of the most challenging skills for students to learn. When a problem requires auxiliary construction, the difficulty of the problem increases drastically, perhaps because deciding which construction to make is an ill-structured problem. By “construction,” we mean adding geometric figures (points, lines, planes) to a problem figure that wasn’t mentioned as "given." |
Recent Additions
|
