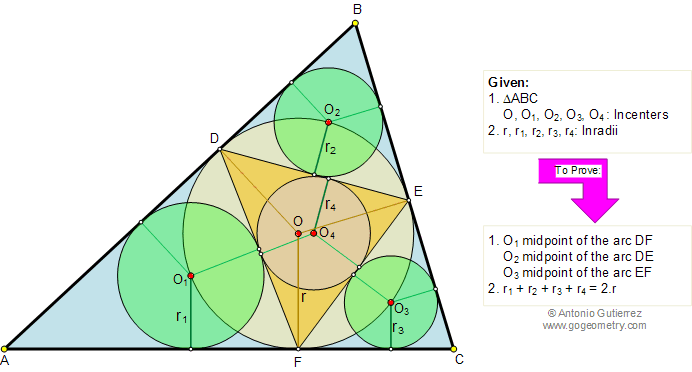
|
The figure shows a triangle ABC with
the contact triangle DEF.
O, O1, O2, O3, and O4 are the
incenters of triangles ABC, ADF, BDE, CEF, and DEF, and r, r1,
r2, r3, and r4 are the inradii,
respectively. Prove (1) O1, O2, O3 are the midpoints of the arcs DF, DE, and EF
respectively, and
(2) r1 + r2 + r3 + r4
= 2.r
View or post a solution.
|
Problem 209. Triangle, Incircles, Inradius, Auxiliary lines