|
Before beginning the solution of
Problem 29, we need to be aware of the following preliminary
propositions:
|
|
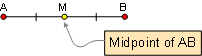
DEFINITION 1. Midpoint is the point on a line
segment dividing it into two segments of equal length.
|
|
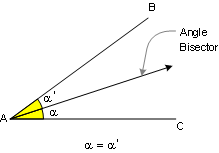
DEFINITION 2. Angle Bisector is a ray that
divides the angle into two congruent adjacent angles.
|
|
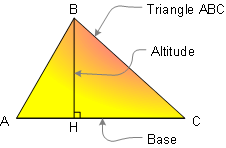
DEFINITION 3. Triangle is a three side polygon.
Polygon is a closed plane figure with
n
sides. Altitude is the perpendicular line segment from
one vertex to the line that contains the opposite side.
|
|
PROPOSITION 1. If two lines are parallel, each pair
of alternate interior angles are congruent. Also converse.
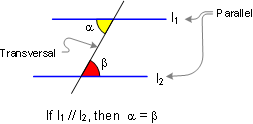
|
|
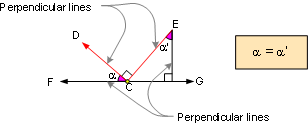
PROPOSITION 2. Two acute angles
are congruent if their sides are respectively perpendicular
to each other.
 |
|
PROPOSITION 3. The sum of the measures of the three
angles of a triangle is 180.
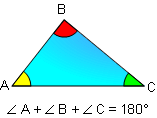
|
|
PROPOSITION 4. The measure of an exterior angle of a
triangle equals the sum of the measures of the two
non-adjacent interior angles.
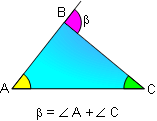
|
|
PROPOSITION 5. The sum of the measures of the acute
angles of a right triangle is 90 (complementary).
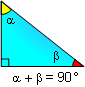
|
|
PROPOSITION 6. Triangle Congruence S.A.S. If two
sides and the included angle of one triangle are congruent to
the corresponding parts of another, then the triangles are
congruent.
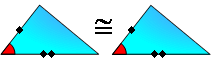
|
|
PROPOSITION 7. Triangle Congruence A.S.A. If two
angles and the included side of one triangle are congruent to
the corresponding parts of another, then the triangles are
congruent.
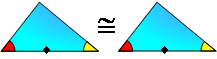
|
|
PROPOSITION 8. Triangle Congruence S.S.S. If
three sides of one triangle are congruent to the three sides of
a second triangle, then the triangles are congruent.

|
|
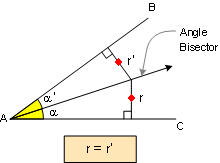
PROPOSITION 9. Any point on the bisector of
an angle is equidistant from the sides of the angle.
 |
|
PROPOSITION 10. If a line is
tangent to a circle, it is perpendicular to a radius at the
point of tangency.
 |
|
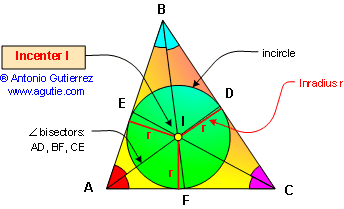
PROPOSITION 11. The bisectors
AD, BF and CE of the angles of a triangle ABC meet in a
point I, which is equidistant from the sides of the
triangle.
The incircle is the inscribed
circle of a triangle. The center of the incircle is called
the incenter, and the radius of the circle is called the
inradius.
|
|
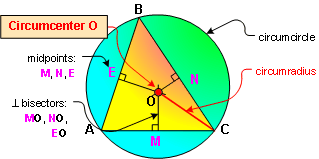
PROPOSITION 12. The circumcenter O of the triangle
ABC is the concurrence point of the three perpendicular
bisectors of the sides. The circumcenter has the same
distance to the three vertices.
|
|
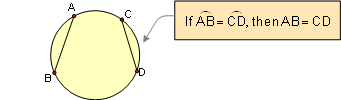
PROPOSITION 13. In the same or congruent circles,
congruent arcs have congruent chords. Also converse.
|
|
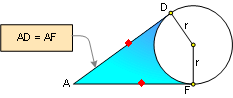
PROPOSITION 14. Two tangent segments to a circle from an
external point are congruent.
|
|
PROPOSITION 15. Isosceles triangle: If two sides of
a triangle are congruent, the angles opposite these sides are
congruent. Also converse.

|
|
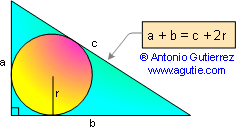
PROPOSITION 16. For a right triangle with catheti (legs) a and
b, the hypotenuse c, and the inradius r: a + b = c + 2r.
|
|
PROPOSITION 17. Right triangle 45-45-90:
the measure of either leg equals one-half the measure of the
hypotenuse time
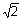 . .
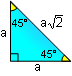
|
|
PROPOSITION 18. A central angle is measured by its
intercepted arc.
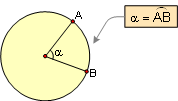
|
|
PROPOSITION 19. An inscribed angle is measured by
one-half its intercepted arc.
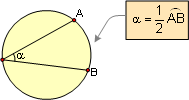
|
|
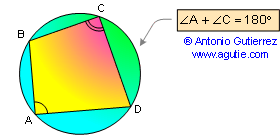
PROPOSITION 20. A cyclic quadrilateral is a
quadrilateral whose vertices all lie on a single circle.
Opposite angles of a cyclic
(inscribed) quadrilateral are supplementary. Also converse.
|
|
|