Clawson Point: Orthic Triangle, Extangents Triangle, Homothecy or Homothety

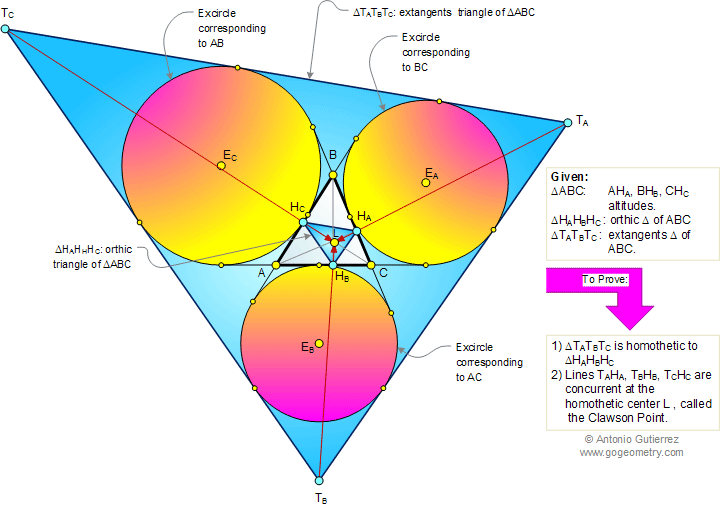
The figure shows a triangle ABC with its orthic triangle H_AH_BH_C, and the extangents triangle T_AT_BT_C. Prove that the triangle T_AT_BT_C is homothetic to triangle H_AH_BH_C, and lines T_AH_A, T_BH_B, T_CH_C are concurrent at the homothetic center L, called the Clawson point.
 

See also:

The Clawson Point Puzzle