The Incas used trapezoids for all their windows and doors, which withstand earthquakes well.

Quadrilaterals: Theorems and Problems 4

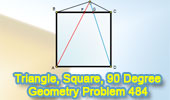Problem 484.
Square, Angle, 90 degrees, Triangle, Measurement, Proportion.

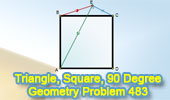Problem 483.
Square, Angle, 90 degrees, Measurement.

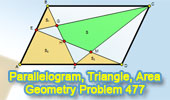Problem 477.
Parallelogram, Triangle, Quadrilateral, Area.

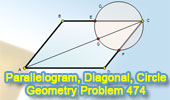Problem 474.
Parallelogram, Diagonal, Circle, Vertex.

Problem 474.
Parallelogram, Diagonal, Circle, Vertex.

Problem 472.
Triangle, Parallel, Side, Parallelogram, Area, Similarity.

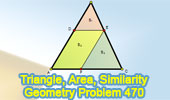Problem 470.
Triangle, Parallel, Side, Parallelogram, Area, Similarity.

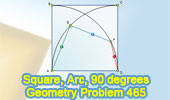Proposed Problem 465.
Square, Arc, Angle, 90 Degrees, Measurement.

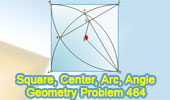Proposed Problem 464.
Square, Arcs, Center, Angle, 90 Degrees, 120 Degrees.

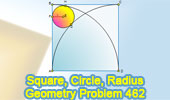Proposed Problem 462.
Square, Arcs, 90 Degrees, Circle, Tangent, Radius, Measurement.

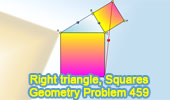Proposed Problem 459.
Right triangle, Squares, Distance, Measurement.

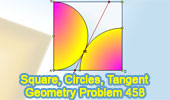Proposed Problem 458.
Square, Semicircle, Circular Sector, Internal Common Tangent, Measurement.

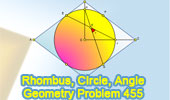Proposed Problem 455.
Rhombus, Inscribed Circle, Angle, Chord, 45 Degrees.

Vecten Outer Point.
 

Proposed Problem 446.
Quadrilateral Area, Dividing the sides into 5 equal parts.

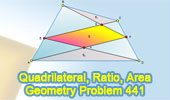Proposed Problem 441.
Quadrilateral, Triangle, Area, Proportion, Measurement, Similarity.

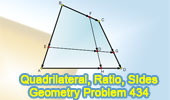Proposed Problem 434.
Quadrilateral, Transversal, Ratio, Measurement, Similarity.

Proposed Problem 433.
Quadrilateral, Triangle, Area, Proportion, Measurement, Similarity.

Proposed Problem 432.
Trapezoid, Parallel, Measurement, Similarity, Transversal.

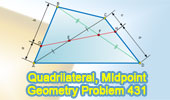Proposed Problem 431.
Quadrilateral, Midpoints of Diagonals, Transversal.

Proposed Problem 425.
Quadrilateral, Triangle, Angles, 10, 20, 50 degrees, Congruence.

Proposed Problem 413.
Cyclic Quadrilateral, Orthocenter, Parallelogram, Concurrency, Congruence.

Proposed Problem 408.
Cyclic quadrilateral, Perpendicular, Parallelogram, Congruence.

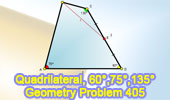Proposed Problem 405.
Quadrilateral, 60, 75, and 135 degrees, Midpoint.

Proposed Problem 337.
Isosceles Trapezoid, Angle bisector, Parallel, Concyclic points.

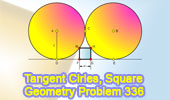Proposed Problem 336.
Two equal circles, a Common Tangent and a Square.

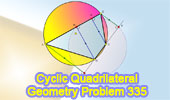Proposed Problem 335.
Cyclic Quadrilateral, Perpendiculars to Sides.

Proposed Problem 334.
Cyclic Quadrilateral, Perpendiculars to Diagonals.

Proposed Problem 331.
Square, Point on the Inscribed Circle, Tangency Points.

Proposed Problem 330.
Cyclic quadrilateral, Perpendicular diagonals, Area, Circumcenter.

Proposed Problem 324.
Quadrilateral with perpendicular diagonals, Concurrence.

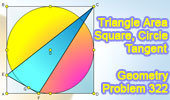Proposed Problem 322.
Square, Inscribed circle, Tangent, Triangle area.

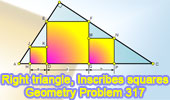Proposed Problem 317.
Right triangle and Inscribed Squares.

Proposed Problem 316.
Circular segments and Inscribed Squares.

Proposed Problem 313.
Circle, Chord, Tangent, Perpendicular, Geometric Mean.

Go to Page: Previous | 1 | 2 | 3 | 4 | 5 | 6 | Next

Last updated: May 7, 2009