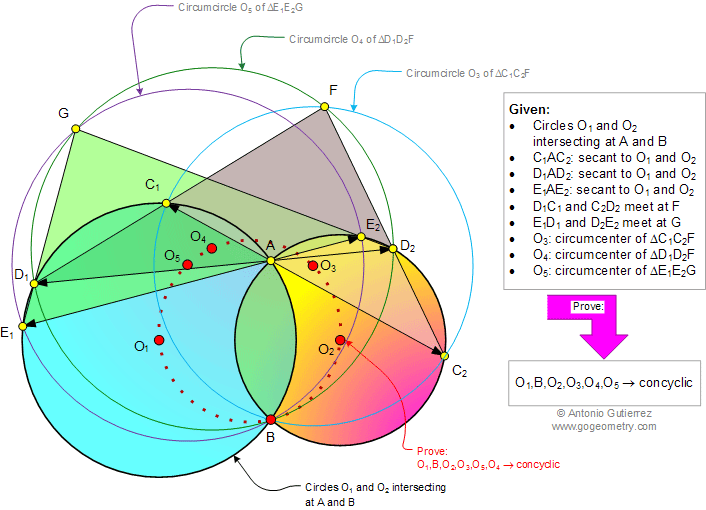
|
The figure below shows circles O1 and
O2 with the secants C1AC2, D1AD2,
and E1AE2. D1C1 and C2D2 meet at F;
E1D1 and D2E2
meet at G.
If O3, O4, and O5 are the
circumcenters of triangles C1C2F, D1D2F,
and E1E2G, respectively, prove that the points
O1, B, O2, O3, O4,
and O5 are concyclic.
|