|
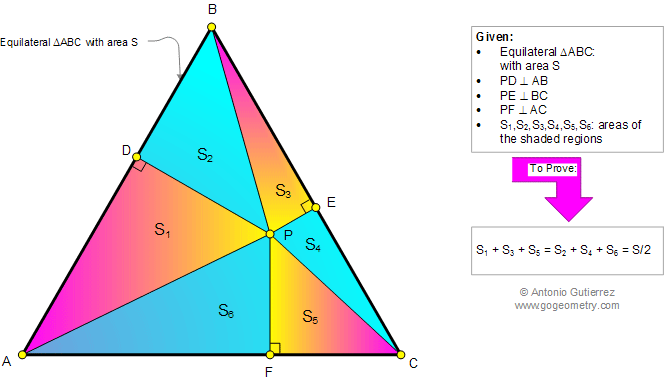
The figure below shows an equilateral
triangle ABC of area S. P is any point and PD, PE, and PF are perpendicular to AB, BC,
and AC, respectively. If S1, S2, S3, S4, S5, and S6 are the areas of the shaded regions,
prove that S1+S3+S5 = S2+S4+S6 = S/2. This entry contributed by Ajit Athle.
|