Geometry Problem 1469: Triangle, Circumradius, Inradius, Midpoints, Arcs, Sum of Distances, Step-by-step Illustration
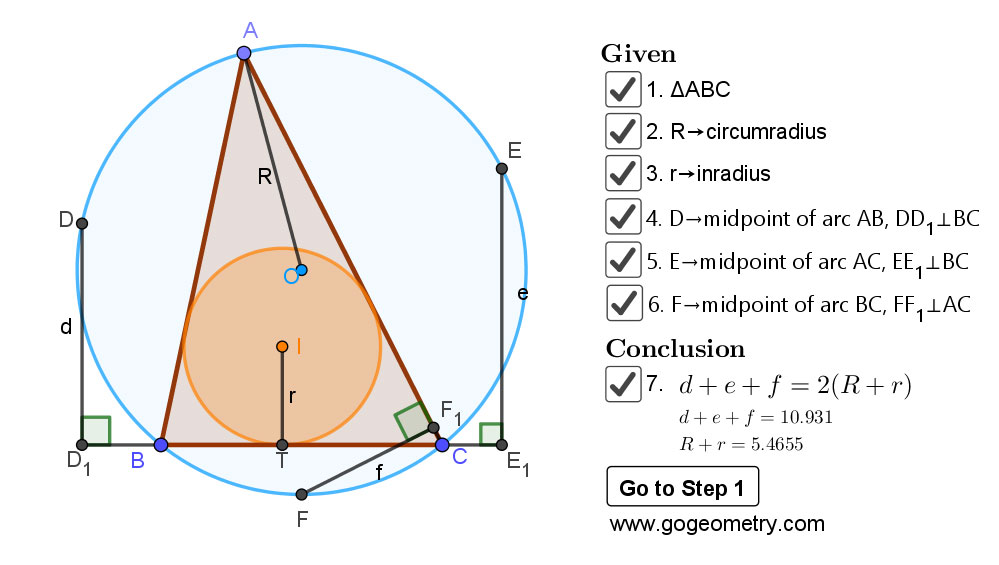
The figure below shows a triangle ABC with the circumradius R, the inradius r. If \(d, e, f\) are the distances from the midpoints of arcs AB, AC, BC to the sides BC, BC, and AC, respectively, prove that \(d+e+f=2(R+r)\).
Static Diagram of Geometry Problem1469
Poster of the Dynamic Geometry 1469 using iPad Apps

Search gogeometry.com
Classroom Resource:
Interactive step-by-step animation using GeoGebra
This step-by-step interactive illustration was created with GeoGebra.
- To explore (show / hide): click/tap a check box.
- To stop/play the animation: click/tap the icon in the lower left corner.
- To go to first step: click/tap the "Go to step 1" button.
- To manipulate the interactive figure: click/tap and drag the blue points or figures.
GeoGebra is free and multi-platform dynamic mathematics software for all levels of education that joins geometry, algebra, tables, graphing, statistics and calculus application, intended for teachers and students. Many parts of GeoGebra have been ported to HTML5.
Recent Additions
Geometry Problems
Open Problems
Visual Index
Ten problems: 1411-1420
All Problems
Triangle
Circle
Triangle Centers
Circumradius, Circumcenter
Inradius, Incenter, Incircle
Midpoint
Perpendicular lines
Circle Tangent Line
Dynamic Geometry
GeoGebra
HTML5 and Dynamic Geometry
iPad Apps
View or Post a solution