Geometry Problem 1384: Triangle, Orthocenter, Circle, Circumcircle, Angle Bisector, 90 Degree
Proposition
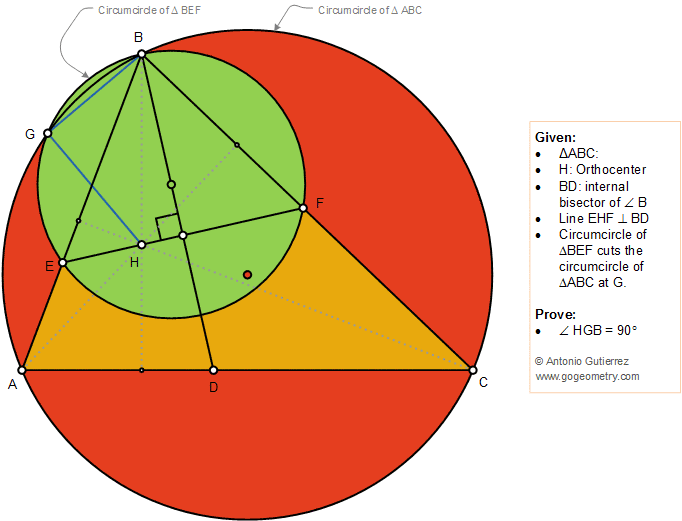
The figure below shows a triangle ABC with the
orthocenter H and the internal bisector BD. Line EHF is perpendicular to
BD. The circumcircle of the triangle BEF cuts the circumcircle of the
triangle ABC at G. Prove that the measure of angle HGB is 90 degrees.
See also
Art of problem 1384
Conformal Mapping or Transformation of Problem
1382
Search gogeometry.com
Recent Additions
Geometry Problems
Ten problems: 1381-1390
Visual Index
Open Problems
All Problems
Circle
Triangle
Angle Bisector
Orthocenter
Circumcircle
90 Degree
View or Post a solution