Geometry Problem 1366: Square, Angle Bisector, Perpendicular, Concyclic Points, Circle, Sketch, iPad Apps.

Proposition

In the figure below, ABCD is a square and E is any point on AD. The bisector of angle EBC meets CD at F. FG is perpendicular to BE (G on BE), AG and BF extended meet at H. Prove that the points A, B, C, H, and D are concyclic (they lie on a common circle).
 


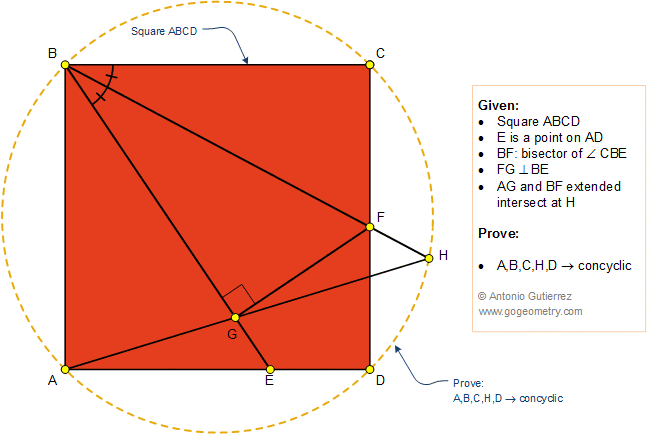
Geometry Problem 1366: Square, Angle Bisector, Perpendicular, Concyclic Points, Circle, Sketch, iPad Apps
 

Sketch and Typography of problem 1366 using iPad Apps


Sketch and typography of Geometry Problem 1366 using iPad Apps, Tutor, Square, Angle Bisector, Perpendicular, Concyclic Points, Circle

 

 

Recent Additions

Geometry Problems
Ten problems: 1361-1370
Visual Index
Open Problems
All Problems
Square
Angle Bisector
Perpendicular lines
Circle
Concyclic Points
View or Post a solution