Geometry Problem 1360: Triangle, Nine-Point Circle, Feuerbach's Circle, Euler's Circle, Cyclic Quadrilateral, Concyclic Points, Sketch, iPad Apps.

Proposition

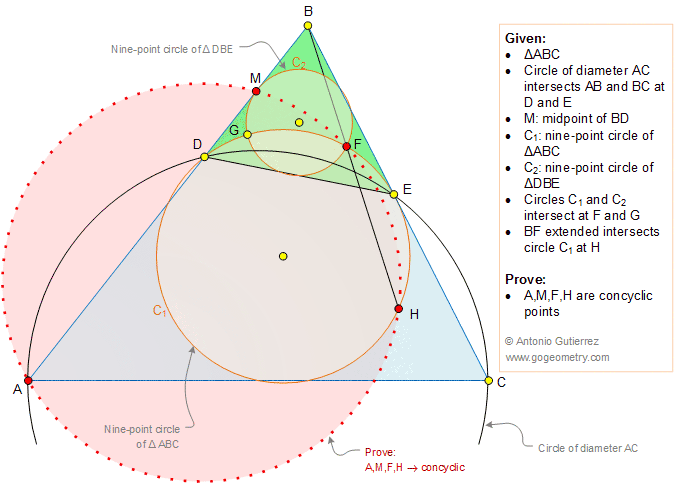
The figure below shows a triangle ABC. Circle of diameter AC intersects AB and BC at D and E, respectively. C₁ is the nine-point circle of triangle ABC and C₂ is the nine-point circle of triangle DBE. Circles C₁ and C₂ intersect at F and G. M is the midpoint of BD and BF extended intersects circle C₁ at H. Prove that the points A, M, F, and H are concyclic.
 

See solution below

 

---

Sketch and Typography of problem 1360 using iPad Apps

See solution below