Geometry Problem 1355: Triangle, Midpoint, Median, Circle, Chord, Equal Product of measure of segments.

Proposition

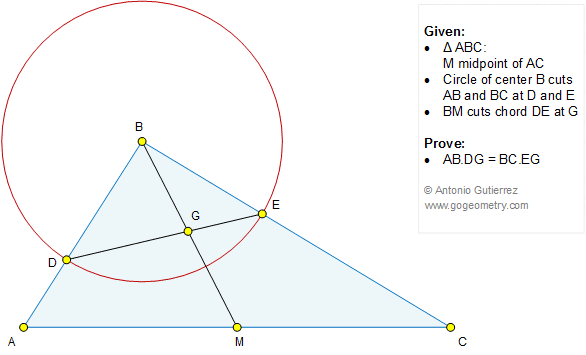
The figure below shows a triangle ABC. M is the midpoint of AC and circle of center B cuts AB and BC at D and E, respectively. BM cuts chord DE at G. Prove that AB.DG = BC.EG.

See solution below

---

Sketch and Typography of Problem 1355

See solution below

---

Geometric Art: Hyperbolic Kaleidoscope of problem 1355 using Mobile Apps

Geometric Art using Mobile Apps

A mobile app or mobile application software is a computer program designed to run on smartphones and tablet computers.

Hyperbolic Kaleidoscope, Poincare Disk Model

Poincare disk model is a model of 2-dimensional hyperbolic geometry in which the points of the geometry are inside the unit disk, and the straight lines consist of all segments of circles contained within that disk that are orthogonal to the boundary of the disk, plus all diameters of the disk. Read more.

See also:
Typography of problem 1355.