Geometry Problem 1351: Two Tangential or Circumscribed Quadrilaterals, Midpoints, Perpendiculars. Math, Tutoring.

Proposition

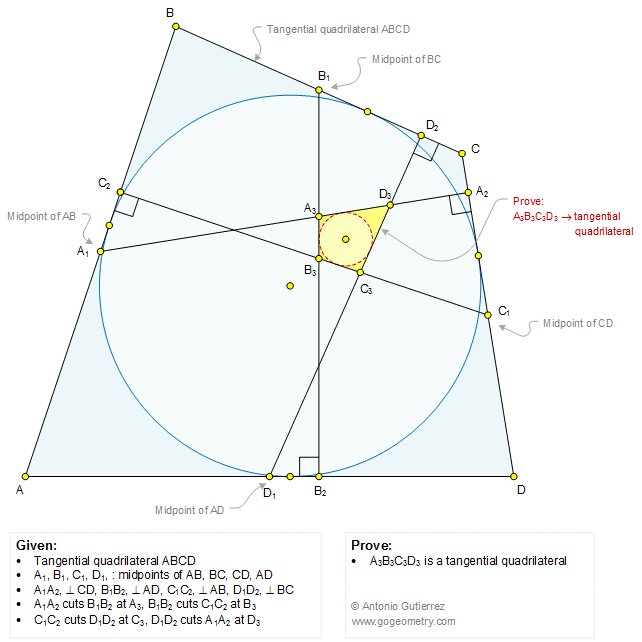
The figure below shows a tangential or circumscribed quadrilateral ABCD. A₁, B₁, C₁, and D₁ are the midpoints of AB, BC, CD, and AD, respectively. A₁A₂, B₁B₂, C₁C₂, and D₁D₂ are perpendicular to CD, AD, AB, and BC, respectively. A₁A₂ cuts B₁B₂ at A₃, B₁B₂ cuts C₁C₂ at B₃, C₁C₂ cuts D₁D₂ at C₃, and D₁D₂ cuts A₁A₂ at D₃. Prove that A₃B₃C₃D₃ is a tangential quadrilateral.

See solution below

---

Poster of Problem 1351: Sketching, Typography, Art using iPad Apps

See solution below

Geometric Art using Mobile Apps

Geometric art is a form of art based on the use and application of geometric figures. A geometric figure is any set or combination of points, lines, surfaces and solids. A mobile app or mobile application software is a computer program designed to run on smartphones and tablet computers.

---

See also:
Art of Problem 1351 using iPad Pro Apps.