Math Infographic, Geometry Problem 1342: Circle, Secant, Chord, Midpoint, Concyclic Points, Cyclic Quadrilateral

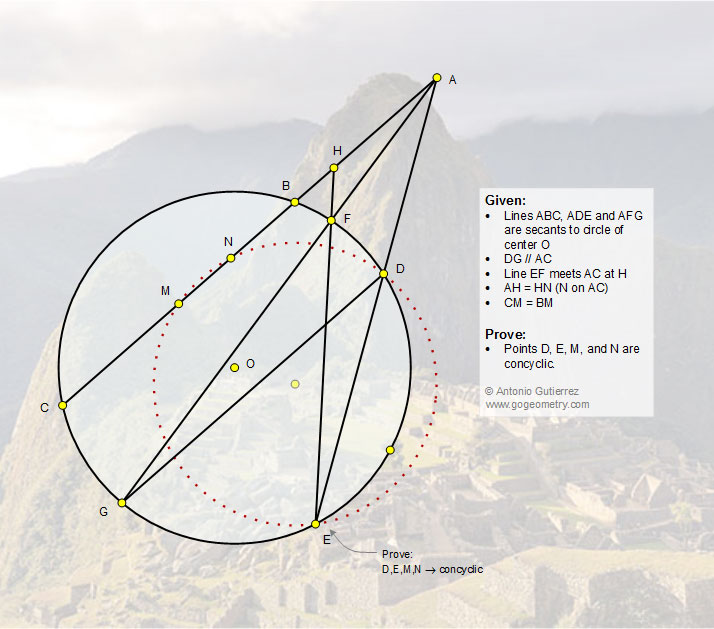
In the figure below, lines ABC, ADE and AFG are secants to a circle of center O so that DG is parallel to AC. Line EF meets AC at H and N is a point on AC so that H is the midpoint of AN. If M is the midpoint of BC, prove that the points D, E, M, and N are concyclic.

See solution below

See also: Hyperbolic Kaleidoscope

Hyperbolic Kaleidoscope of Problem 1341 on Instagram:

#Geometric Art of Problem 1341: #Isosceles Triangle, 80-20-80 Degrees, #Hyperbolic Kaleidoscope, #iPad Apps #Geometry Details: http://www.gogeometry.com/school-college/4/p1341-ipad-hyperbolic-kaleidoscope-isosceles-sw.htm

A post shared by Antonio Gutierrez (@gogeometry1) on Aug 10, 2017 at 1:08pm PDT

---