Math Infographic, Geometry Problem 1340: Triangle, Incenter, Concentric Circles, Isosceles Triangles, Congruence

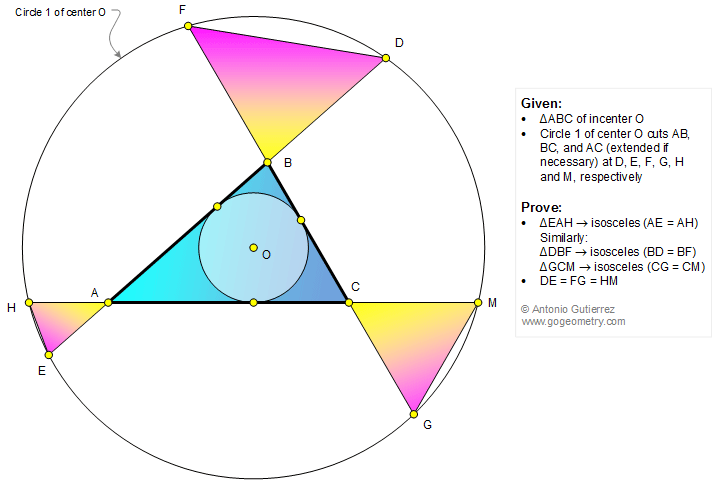
O is the incenter of a triangle ABC. A circle of center O cuts AB, BC, and AC (extended if necessary) at D, E, F, G, H, and M, as shown in the figure below. Prove that (1) the triangle EAH is isosceles (AE = AH), similarly, the triangles DBF and GCM are isosceles; (2) DE = FG = HM.

See solution below

---

---