Geometry Problem 1301: Arbelos, Semicircles, Diameters, Circle, Incircle, Incenter, Square, Midpoint, Concurrency. Level: School, College, Mathematics Education

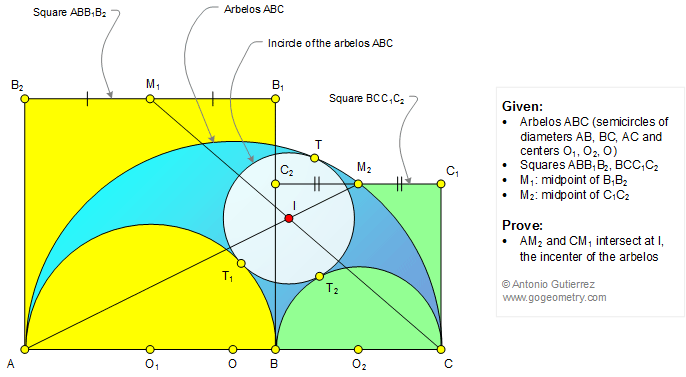
The figure below shows an arbelos ABC (AB, BC, and AC are semicircles of centers O₁, O₂, and O) and the squares ABB₁B₂ and BCC₁C₂. If M₁ and M₂ are the midpoints of B₁B₂ and C₁C₂, respectively, prove that AM₂ and CM₁ intersect at I, the incenter of the arbelos.  
 

  
See also:
Typography of problem 1301