|
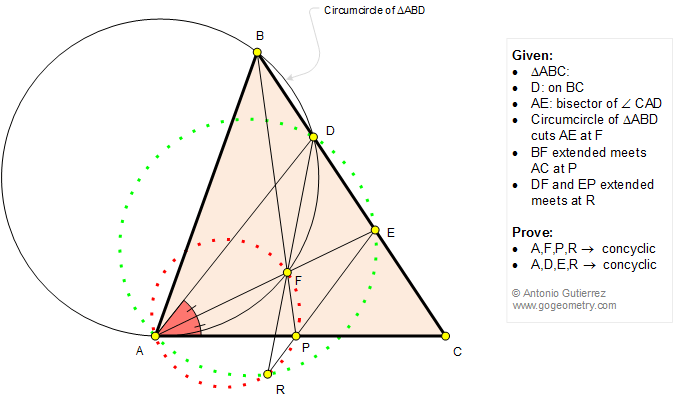
D and E lie on BC of a triangle ABC such that AE bisects
angle DAC (see the figure),
The circumcircle of triangle ABD cuts AE at F and BF meets AC at P.
DF and EP (extended) meet at R.
Prove that (1) Points A, F, P, and R are concyclic; (2) Points A, D, E, and R are concyclic.
This entry contributed by Sumith Peiris, Moratuwa, Sri Lanka.
|

