Geometry Problem 1132: Triangle, Excircle, Tangency Point, Parallel, Midpoint. Level: High School, SAT Prep, Honors Geometry, College, Math Education

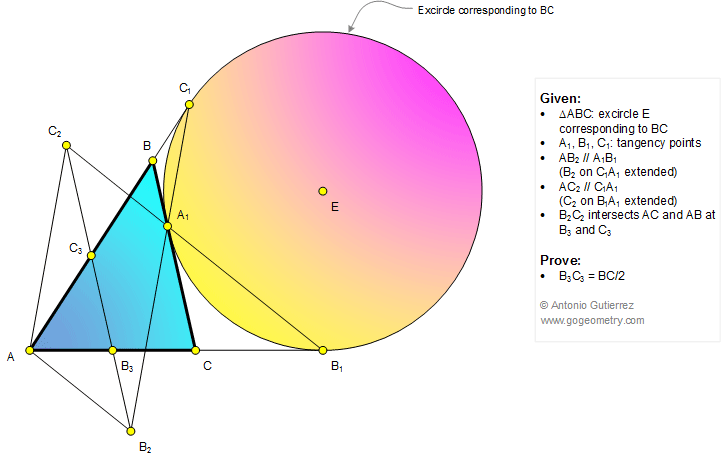
In a triangle ABC (figure below), the excircle E corresponding to BC is tangent to AB, BC, and AC at C₁, A₁, and B₁, respectively. AB₂ is parallel to A₁B₁ (B₂ on C₁A₁ extended), AC₂ is parallel to C₁A (C₂ on B₁A₁ extended). B₂C₂ intersects AC and AB at B₃ and C₃, respectively. Prove that B₃C₃ = BC/2.