Geometry Problem 1118: Right Triangle, Angle Trisection, Concyclic Points, Cyclic Quadrilateral. Level: High School, SAT Prep, Honors Geometry, College, Math Education

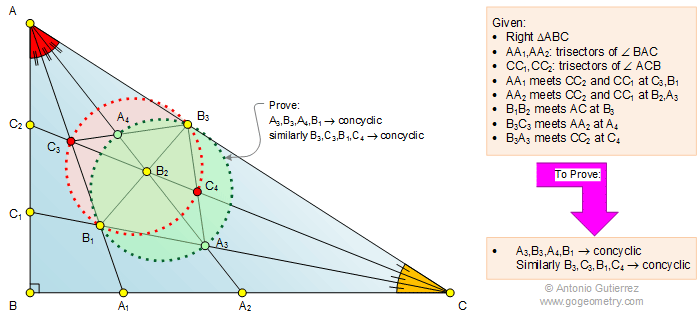
The figure below shows a right triangle ABC with AA₁ and AA₂ trisectors of angle BAC, similarly CC₁ and CC₂ trisectors of angle ACB. AA₁ meets CC₂ and CC₁ at C₃ and B₁, respectively. AA₂ meets CC₂ and CC₁ at B₂ and A₃, respectively. B₁B₂ meets AC at B₃, B₃C₃ meets AA₂ at A₄, and B₃A₃ meets CC₂ at C₄. Prove that A₃, B₃, A₄, B₁ are concylic points, similarly B₃, C₃, Bv, C₄ are concyclic points.