Problem 1103: Right Triangle, Incircle, Inscribed Circle, Radius, Geometric Mean, Sangaku, Japanese, Metric Relations. Level: High School, SAT Prep, College Geometry

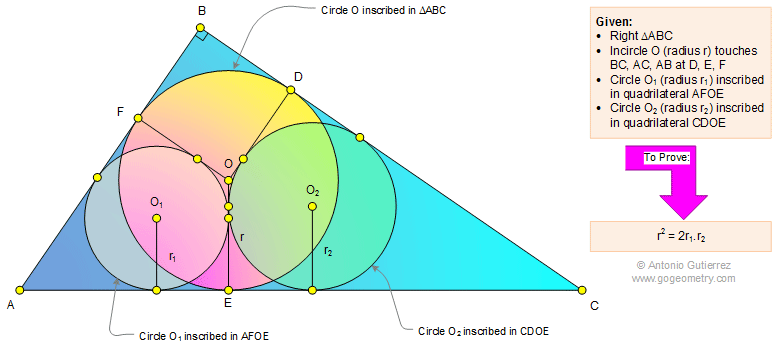
In a right triangle ABC (see the figure below) incircle O (radius r) is tangent to BC, AC, and AB at D, E, and F, respectively. Circle O₁ (radius r₁) is inscribed in quadrilateral AFOE and circle O₂ (radius r₂) is inscribed in quadrilateral CDOE. Prove that r² = 2r₁.r₂.


 

See also:
Art and typography of problem 1103.