|
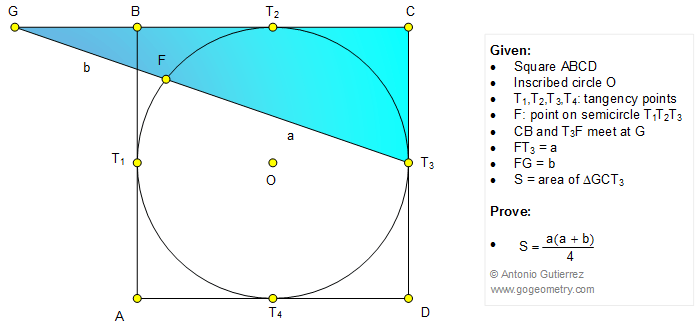
In the figure ABCD is a square and circle O
is tangent to AB, BC, CD, and AD at T1, T2, T3, and T4,
respectively. F is a point on the semicircle T1T2T3, and lines
CB and FT3 meet at G. If FT3 = a, FG = b, and S is the area of
triangle GCT3, prove that S = a(a+b)/4.
|