|
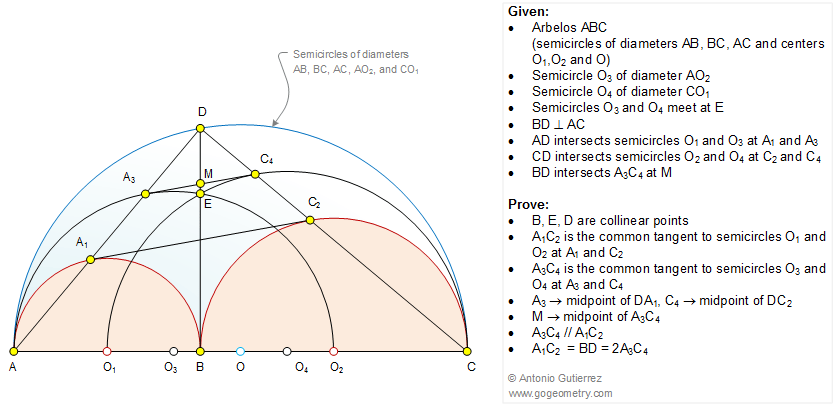
The figure shows an arbelos ABC (AB, BC, and AC are semicircles
of centers O1, O2, and O). The semicircles
of diameters AO2 (center O3) and CO1 (center O4)meet at E. BD is perpendicular to AC,
AD intersects semicircles O1 and O3 at A1
and A3, respectively, CD intersects semicircles O2 and O4 at C2 and
C4, respectively. Prove that (1) B, E, D are
collinear points; (2) A1C2 is
the common tangent to semicircles O1 and O2 at A1 and C2,
respectively; (3) A3C4 is the common tangent to
semicircles O3
and O4 at A3 and C4, respectively;
(4) A3 is the midpoint of DA1 and C4
is the midpoint of DC2; (5) M is the midpoint of A3C4; (6) A3C4
// A1A2; (7) A1C2
= BD = 2A3C4. See also:
Artwork Problem
1071.
|