Infographic Geometry Problem 1058: Triangle, Sum of the Areas, Altitude, Perpendicular, Circumcircle, Circle, Diameter. Level: High School, SAT Prep, College, Mathematics Education

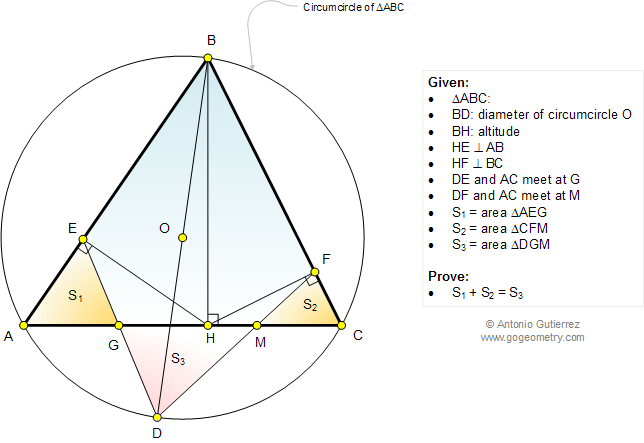
In a triangle ABC, BH is the altitude and BD is a diameter of the circumcircle O (see the figure below). HE and HF are perpendicular to AB and BC at E and F, respectively. DE and DF meet AC at G and M, respectively. If S₁ = area of triangle AEG, S₂= area of triangle CFM, and S₃ = area of triangle DGM, prove that S₁ + S₂ = S₃.