|
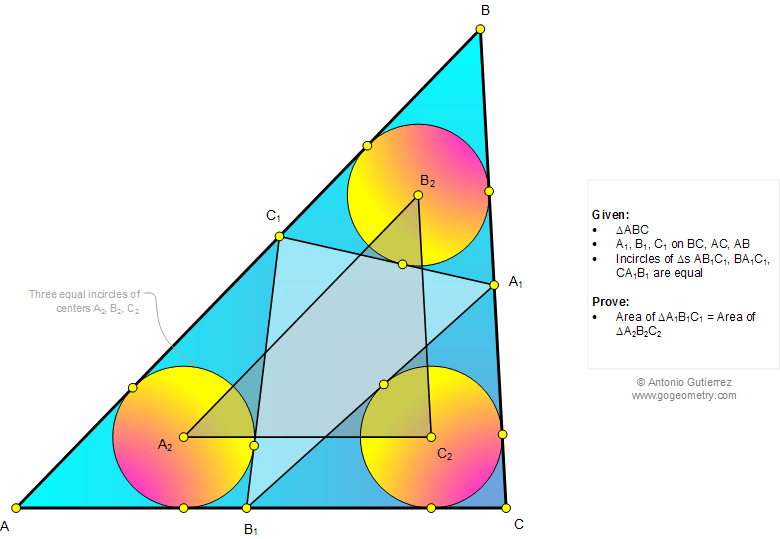
The figure below shows a
triangle ABC where A1, B1, and C1 are on BC, AC, and AB,
respectively, so that the
incircles
of triangles AB1C1, BA1C1, and
CA1B1 are equal. Prove that the
areas
of triangles A1B1C1 and A2B2C2
are equal (equivalent triangles).
|

