|
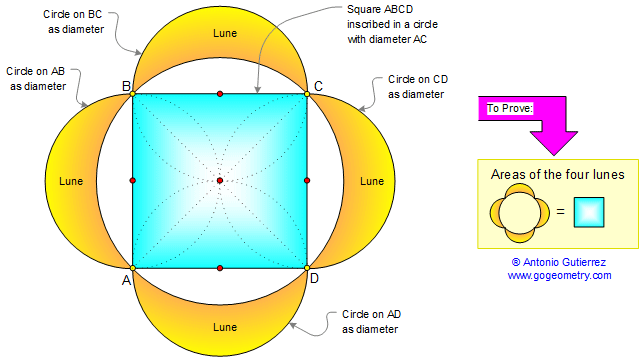
In the figure below, the sum of
the areas of the four lunes equals the area of the square.
A lune is a plane figure bounded by two circular arcs of unequal
radii.
The fact that the areas bounded by
arcs were independent of Pi (π) led Hippocrates to continue the hopeless search for a
method of squaring the circle.
Hippocrates of Chios (c.470 BC -
c.410 BC) was a Greek mathematician who worked on the classical
problems of squaring the circle and duplicating the cube.
Squaring the circle or the
quadrature of the circle is one of the three great
problems of Classical Geometry. It is the challenge to construct
a square with the same area as a given circle by using only a
finite number of steps with compass and straightedge.
See also:
Hippocrates 1,
Hippocrates 2,
Hippocrates 3,
Hippocrates 4,
Pythagoras and
Circle Area,
Similar
shapes.
Home |
Geometry |
Pythagoras Index
|
Right Triangle Formulas |
Lune Index |
Square area |
Email | By Antonio Gutierrez
|