|
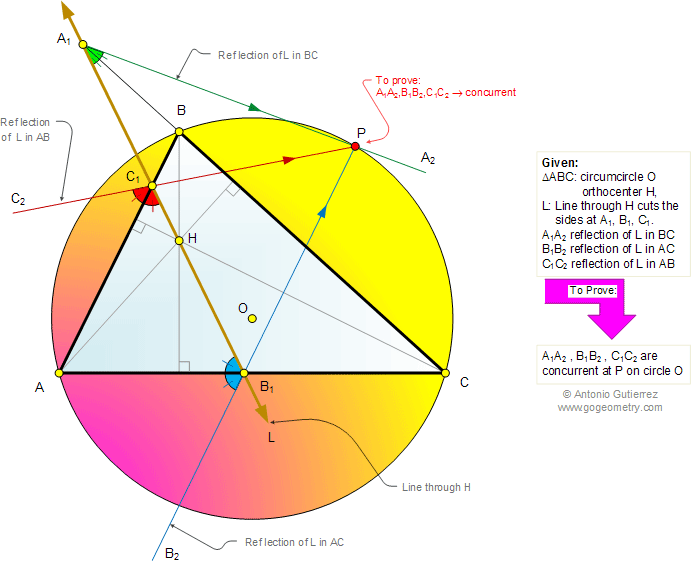
The figure shows a triangle ABC. L is a line through
the orthocenter H that cuts
the sides at A1, B1, and C1. Lines A1A2,
B1B2, and C1C2 are the
reflection of L in sides BC, AC, and AB, respectively. Prove that A1A2,
B1B2, and C1C2 are
concurrent at a point P on the circumcircle O.
|