|
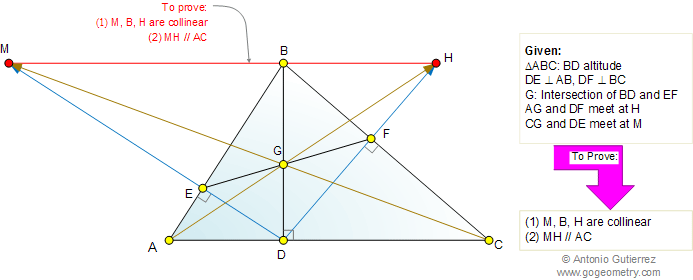
The figure shows a triangle ABC with the
altitude BD. DE is perpendicular to AB and DF is perpendicular to BC. BD
and EF meet at G. Lines AG and DF meet at H, lines CG and DE meet at M.
Prove that (1) the points M, B, and H are collinear; (2) MH is parallel
to AC.
|