|
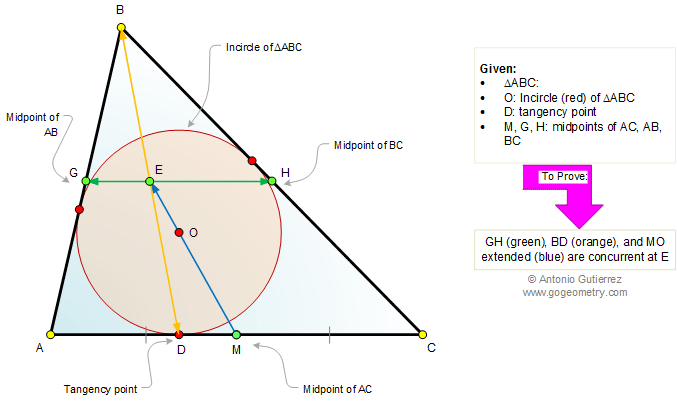
The figure shows a triangle ABC with the
incircle O tangent to AC at D. Points M, G, and H are the midpoints of AC, AB,
and BC, respectively. Prove that lines GH, BD, and MO extended are
concurrent at the same point E.
See also:
Sketch of problem 592
|