Math: Geometry Problems 534. Activate Flash plug-in or JavaScript and reload to view
the Math Geometry Proposed Problems, online geometry classes, Geometry help,
College, Online Learning. Site created and maintained by Antonio
Gutierrez.
Problem 534: Right Triangle, Squares, Perpendicular, Dissection, Areas. Level: High School, SAT Prep, College
Geometry
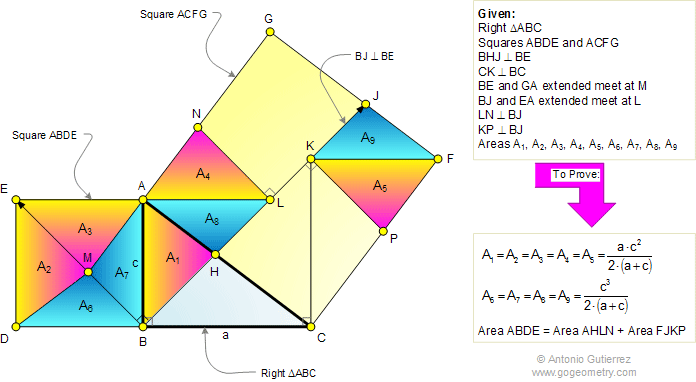
The figure shows a right triangle ABC (BC =
a, AB = c) with the squares ABDE and ACFG. Line BHJ is perpendicular to
BE. Line CK is perpendicular to BC. Lines BE and GA extended meet at M.
Lines BJ and EA extended meet at L. Lines LN and KP are perpendicular to
BJ. If A1, A2, A3, A4, A5,
A6, A7, A8, and A9 are the
shaded areas, prove that (1)
,
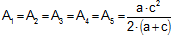(2)
,
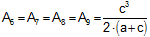(3) Area ABDE = Area AHLN + Area FJKP.
,
(2)
,
(3) Area ABDE = Area AHLN + Area FJKP.
